| |
Elegant Mathematics Assessed “Awardable” for DARPA ERIS Marketplace
ML-Tensor-Boltzmann Approach for Disrupting Computational Complexity in Advanced CFD Tasks |
Elegant Mathematics, a leading provider of mathematics-driven R&D across science and engineering, announced that it has achieved
“Awardable” status through DARPA Expedited Research Implementation Series (ERIS) Marketplace.
Elegant Mathematics solutions are designed to overcome the computational bottlenecks that limit today’s most advanced simulations. The company’s flagship innovation — a
novel ML-Tensor-Boltzmann approach — redefines computational fluid dynamics (CFD) by enabling high-fidelity modeling across extreme physical regimes previously deemed intractable.
Our video,
ML-Tensor-Boltzmann Approach for Disrupting Computational Complexity in Advanced CFD Tasks, accessible only by government customers on the
DARPA ERIS Marketplace, presents a real-world use case where the
company’s method revolutionizes computational fluid dynamics by
solving the Boltzmann equation with unprecedented efficiency — enabling high-fidelity simulations in extreme environments and under highly challenging conditions.
Elegant Mathematics was recognized among a competitive field of applicants to the ERIS Marketplace whose solutions demonstrated innovation and potential impact on DoD missions.
Government customers interested in viewing the video solution can create an ERIS Marketplace account at
darpaconnect.us/eris
Key advantages: efficient across extreme regimes: applicable to high Reynolds, Knudsen, and Mach numbers;
scales with problem complexity: linear dependence on Reynolds number vs. cubic in traditional methods;
radically reduced compute time: multiple orders-of-magnitude faster for high-Reynolds-number regimes
Key principles:
- Full 3D Velocity Space Representation: We solve the Boltzmann equation by discretizing each finite element with a complete three-dimensional velocity space.

- Tensor Decomposition for Memory Efficiency: The velocity space is approximated using tensor decomposition, reducing memory requirements per spatial cell from cubic to linear complexity.
- Advanced Correlation and Compression: We further correlate and approximate the one-dimensional factors of the tensor decomposition across neighboring spatial cells, leveraging compressed sensing techniques. This reduces computational complexity to just a few numbers per finite element.
Breakthrough Performance
This approach enables solving the Boltzmann equation with computational complexity per spatial cell comparable to Navier-Stokes, but without the prohibitive grid refinement required for high Reynolds numbers, shock waves, high Mach numbers, or large Knudsen numbers. Our method guarantees convergence even in these challenging regimes.

Proven Applications
Our method has been validated across diverse, high-impact scenarios:
- Extreme Pressure Gradients: Successfully modeled UF₆ centrifuge flows with pressure gradients spanning 8 orders of magnitude, requiring only ~100 discrete cells along the gradient, compared to ~10,000 cells for classical methods.
- Plasma Dynamics: Effectively solves the Vlasov equation for plasma modeling, with successful applications in particle beam dynamics.
- Supersonic Combustion: Accurately captures combustion in model turbojet engine problems at supersonic speeds.
Why It Matters
Our method delivers unparalleled computational efficiency and accuracy, enabling simulations of complex physical phenomena with drastically reduced resources. This makes it a game-changer for applications in aerospace, plasma physics, and high-speed combustion, aligning with DARPA’s mission to advance transformative technologies.
A Fully Autonomous Flying Wing for Disaster Response and Beyond
At
Elegant Mathematics, we’ve crafted a
fully autonomous flying wing that redefines exploration.
Compact, lightweight, and agile, this drone operates without human input or external control, thriving in high-risk, GPS-denied, and human-inaccessible environments — like collapsed buildings, underground facilities, and disaster zones.
With
no reliance on GNSS, Wi-Fi, or LTE, the drone executes complete missions on its own: navigating, sensing, analyzing, and reporting in real time.
Its
modular multi-sensor architecture includes radar, acoustic surface mapping, and hyperspectral imaging — all fused onboard to generate a precise 3D semantic model of the environment.
Our platform integrates
deterministic segmentation algorithms and low-power embedded computing to deliver high-performance autonomous perception. It is designed from the ground up to be
cost-effective, scalable, and resilient — making it ideal for both emergency and tactical missions.
1.Proven in the Field: DARPA Triage Challenge
Our drone platform is currently undergoing real-world testing as part of the prestigious
DARPA Triage Challenge, where we participate for the second consecutive year as the
MR NIB (Multi-modal-Research Non-Invasive-Beam) team. The competition tasks autonomous systems with identifying and prioritizing casualties in disaster zones, requiring fast, accurate, and reliable detection under extreme conditions. Our fully operator-free drone, equipped with multimodal sensors and onboard AI, is designed precisely to meet these challenges.
Learn more about the DARPA Triage Challenge, its mission and participating technologies by clicking the image below.
2. Problem We Solve
In natural disasters, war zones, and industrial accidents,
every second matters. The speed and safety of response operations can determine whether lives are saved or lost. Yet current UAV systems remain constrained: they require human operators, stable communications, and often provide only raw data that must be analyzed manually — wasting valuable time.
Our solution changes that.
- No operator required — completely autonomous flight enables immediate deployment with no need for skilled pilots or remote control links.
- Operates in collapsed, cluttered, or GPS-denied environments, where traditional drones fail or cannot navigate safely.
- Detects human presence and materials beneath debris, providing first responders with vital situational awareness before entering hazardous zones.
- Delivers reliable, high-resolution 3D data in real time, enabling faster triage decisions and more effective mission planning.
By removing the human operator from the loop and automating perception onboard, our drone
dramatically reduces response time and risk to personnel — delivering intelligent, multi-modal situational awareness into hazardous environments when it matters most.
3. Our Technology
At the heart of our system is a sub-kilogram drone that operates without a human pilot or ground control. It navigates autonomously in unpredictable, cluttered, and GPS-denied environments — such as collapsed buildings or underground shafts — by leveraging a tightly integrated set of custom sensors and edge-optimized processing pipelines.
Multi-modal Sensing and Data Fusion
Our sensing and data fusion architecture includes:
- Microphone arrays and barometric differentials to reconstruct local air flows and determine 3D velocity vectors and drift due to wind or turbulence.
- Acoustic echolocation and ultrawideband radar to build a real-time map of nearby surfaces, even in complete darkness, fog, or dust. These signals allow us to generate local 3D geometry with centimeter-level accuracy in all directions.
- Hyperspectral video imaging, mapped onto the reconstructed 3D surfaces, provides rich material classification and context-aware texture information — enabling detection of biological signatures, synthetic materials, or changes over time.
- Internal odometry and tight sensor fusion ensure robust dead reckoning without relying on GPS, vision, or magnetometers.
Efficient and Deterministic Perception
Unlike many AI-dependent systems, our solution deliberately avoids large neural networks during flight. Instead, we exploit known physical priors: once the 3D structure of the nearby environment is mapped, many segmentation tasks can be resolved deterministically with minimal compute overhead.
This approach allows us to run all critical algorithms in real time on board using low-power components, without relying on external infrastructure or high-throughput datalinks.
Our current platform features a flying wing design equipped with a dual-axis gimbal-mounted motor. This configuration enables vertical take-off and landing, while also providing excellent efficiency for long-range flights.
Flying over a test structure — a staircase embedded in a forested landscape — in complete darkness, light fog, and at a speed of approximately 5 m/s,
our system successfully detected the shape of the staircase steps, preserving their 3D geometry in STL and STEP formats.
4. Autonomous Navigation and Swarm Intelligence
Our drone platform operates with full flight autonomy — no human operator required. The system continuously processes multimodal data in real time through a four-stage autonomy stack:
- Initial Estimation:
MEMS-based IMUs and barometric sensors determine spatial orientation and ambient wind speed.
- Surface Mapping:
Radar and acoustic echoes are used to construct the geometry of nearby objects and environments.
- 3D Reconstruction:
Hyperspectral imaging is fused with geometric data to deterministically reconstruct textured 3D models, enabling rapid and accurate environmental understanding.
- SLAM Completion:
All sensor modalities are integrated into a final SLAM layer, allowing for precise, drift-free navigation and mission planning.
In swarm configurations, multiple drones share telemetry and environmental data via radar and ultrasonic reflections. This creates a cooperative sensing network that enhances range, reliability, and resolution — even in complex or degraded environments. The result is a scalable, resilient system capable of collective intelligence without centralized control.
5. Energy Efficiency and Onboard AI
To support untethered operations in the field, our platform is designed for extreme onboard efficiency. The drone uses a heterogeneous computing architecture combining ARM cores, DSPs, FPGAs, and NPUs, capable of over
100 GFLOPS and 50 TOPS of performance.
We follow a deterministic, hardware-friendly approach:
- Acoustic and radar signals are used to segment surfaces in the environment.
- Hyperspectral imaging is then applied only to relevant regions, reducing the computational load.
- This selective pipeline avoids the need for cloud-based AI and large models — enabling operation using inexpensive, energy-efficient hardware.
Thanks to this approach, our drones can generate and store dense multimodal 3D representations using as little as
100 kB per square meter, with up to
1 TB of onboard memory. The system automatically ignores inputs from degraded sensors (e.g., visible-spectrum cameras at night) to conserve energy, making it reliable under variable and challenging conditions.
6. Dual-Use Potential
Our technology was originally conceived to support urgent humanitarian response in disaster zones — and it is here that its civilian applications are most immediate and impactful. Our drone can fly over collapsed buildings, unstable terrain, or hazardous industrial sites to autonomously map the area and detect human presence without placing rescue teams at risk. This makes it a powerful tool for
emergency services, mining companies, and environmental monitoring agencies that need accurate situational awareness in areas too dangerous or inaccessible for humans.
At the same time, the system's autonomy, reliability, and ability to operate without GPS or operator input make it highly relevant for
defence and security applications. In military or border surveillance contexts, it can provide near-instantaneous mapping and detection of life signs in complex terrain, dense forests, or underground shelters. The use of low-SWaP (Size, Weight, and Power) components ensures stealth and long endurance — ideal for
tactical intelligence gathering, combat casualty search, and infrastructure inspection in conflict zones.
Our system is built on a modular and scalable architecture, designed for seamless adaptation to new sensing payloads and mission profiles. Its fully autonomous operation and sensor-driven intelligence allow it to be deployed in complex environments without reliance on external infrastructure. This flexibility reflects
our core philosophy: to deliver advanced aerial capabilities in a compact, cost-effective, and field-ready solution.
Our autonomous drone platform is changing the future of emergency response and tactical missions. Join us in advancing this groundbreaking technology for a safer and more efficient world.
When It Counts, We Count on Elegant Mathematics
Complex problems don’t need 10,000 lines of code.
They just need the right ten.
That’s where
elegance meets execution — and where we build systems that deliver.
Discover our array of ready-made solutions designed to meet the highest standards of quality and technical advancement.
1. Accelerate with Ready-Made Solutions
Minimize development time by choosing from our ready-made solutions, adaptable to your needs within just 3-4 months:
1.1. Software Solutions for Inverse Problems of Maxwell's Equations
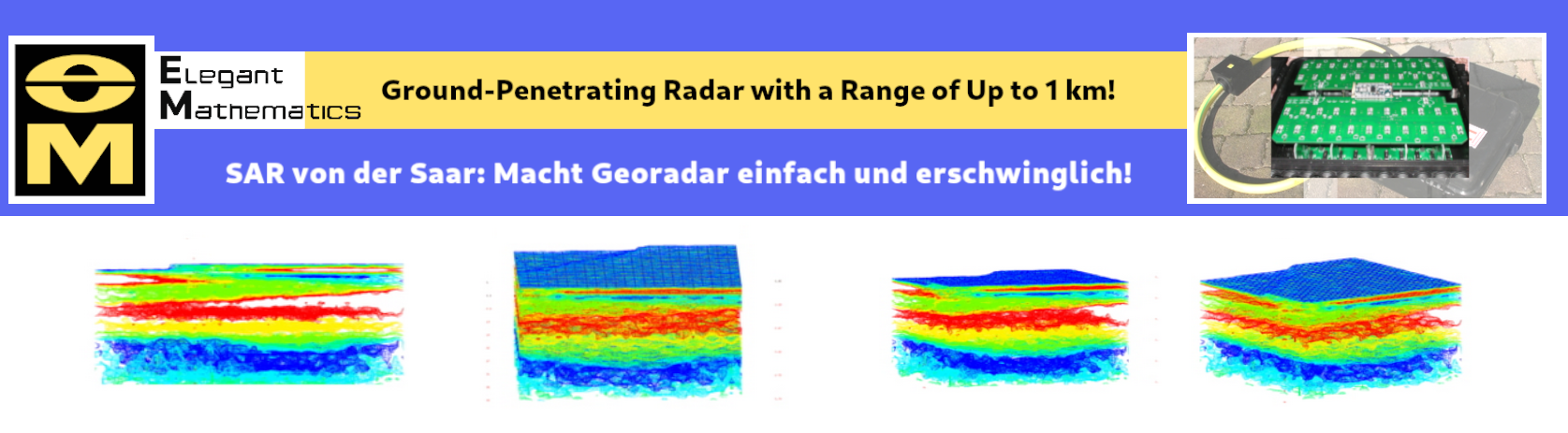
We have extensive experience in solving inverse problems of geometrical optics and Maxwell's equations. Our company has developed specialized software libraries that we successfully use for modeling and solving practical problems. For example, our technologies are used for data processing in ground-penetrating radars developed by our company (
https://www.sar-saar.com/), as referenced in the article (doi: 10.1109/IWAGPR.2011.5963843).
1.2. Software Solutions in Fluid Dynamics
Modern software packages can numerically predict laminar or weakly turbulent fluid flows using the discretization of Navier-Stokes equations. However, modeling highly turbulent flows with Reynolds numbers above 10000 or flows with high Knudsen numbers remains a challenging task. Most existing solutions require substantial computational resources, limiting their use even on powerful supercomputers.
Our methods for solving the adaptive Boltzmann equation using multilinear (tensor) approximations (doi: 10.1007/s00607-002-1458-9, 10.1002/pamm.200700641, 10.1002/pamm.200700839) enable the modeling of physical processes that are inaccessible to Navier-Stokes equation solvers. These methods are effective in modeling flows with varying velocity directions or average temperatures at close distances.
Our solutions are used for tasks such as predicting the shape of turbomolecular pump blades (down to 10
-12 Torr), optimizing mass spectrometer tracts (down to 10
-10 Torr), predicting the shapes of HPLC/UHPLC valves (1000-5000 Bar), optimizing chemical reactor shapes, including those with supercritical fluids, and other complex tasks where traditional numerical methods do not provide the required accuracy.
1.3. Modules for Automated Microscopy and Biological Analysis
Uncover the hidden details of biological specimens with our cutting-edge Modules for Automated Microscopy. These modules integrate advanced imaging technology with powerful statistical analysis, enabling you to extract valuable insights from complex biological samples. From particle size distribution analysis to intricate statistical evaluations, our modules empower you to push the boundaries of scientific discovery. Let our technology illuminate the microscopic world and unveil the secrets it holds.
1.4. Auto Samplers
Are you looking to streamline sample handling and processing? Our Auto Samplers are meticulously designed to enhance efficiency and accuracy in your laboratory workflow. These automated systems are capable of handling a wide range of sample types and sizes. Through precise automation, we ensure consistent and reproducible results, significantly reducing human error and freeing up valuable time for your team. Whether it's in the field of chemistry, biology, or beyond, our Auto Samplers bring a new level of precision to your scientific endeavors.
1.5. Turbo Molecular Pump Control Modules
In the realm of vacuum technology, our Turbo Molecular Pump Control Modules stand as paragons of precision and control. These modules provide comprehensive management of turbo molecular pumps, ensuring optimal performance and longevity. With sophisticated algorithms and real-time monitoring, these modules regulate pressure, temperature, and other critical parameters, maintaining a stable and controlled vacuum environment. Experience peak efficiency and reliability in your vacuum systems with our Turbo Molecular Pump Control Modules.
1.6. Precision Voltage Control for Mass Spectrometers
Elevate your mass spectrometry experiments to unprecedented accuracy with our Precision Voltage Control Modules. Offering the ability to precisely manipulate voltage within the microsecond range, these modules redefine the capabilities of your mass spectrometers. With programmable waveform shaping and synchronization across multiple channels, our technology enables you to achieve exceptional precision in ionization processes. Take control of your experiments with the utmost confidence and precision.
1.7. Metal Oxide Sensor-Based Monitoring Systems
Safeguard your industrial spaces and operations with our Metal Oxide Sensor-Based Monitoring Systems. These cutting-edge systems utilize advanced metal oxide sensors to detect and identify industrial gases and leaks in real-time. From gas concentration monitoring to rapid identification of hazardous substances, our monitoring systems enhance workplace safety and environmental compliance. Gain real-time insights and ensure a secure working environment with our Metal Oxide Sensor-Based Monitoring Systems.
2. Key Solutions for Ambitious Goals
For more extensive requirements, our range of products is available within 6-8 months, meticulously tailored to your exacting demands:
2.1. High-Voltage Blocks for Radiochemistry
Are you embarking on ventures that demand unparalleled precision and control over high-voltage processes? Our High-Voltage Blocks for Radiochemistry are engineered to meet the most demanding requirements of your radiochemical applications. With voltage ranges reaching up to 100 kV, these specialized blocks ensure reliable and stable performance under extreme conditions. Whether it's in nuclear research, particle acceleration, or experimental setups requiring high-voltage components, our blocks empower you with a crucial edge in your endeavors. Count on our expertise to deliver the high-voltage solutions you need for success.
2.2. Mechanical Drive and Control Systems
From chromatography to mass spectrometry, the heart of precision lies in meticulous mechanical control. Our Mechanical Drive and Control Systems offer a symphony of precision engineering, enabling you to orchestrate movements with utmost accuracy. These systems seamlessly integrate with various scientific instruments, providing smooth and reliable mechanical drives for diverse applications. Paired with sophisticated control software, our systems grant you the power to fine-tune and optimize experimental setups with ease. Elevate your mechanical precision and embark on a new era of experimental mastery.
3. Boldly Embrace the Future with Us
In 12 to 15 months, we offer integrated solutions capable of truly transforming your business:
3.1. Comprehensive Chemical Platforms
Experience chemistry on a whole new level with our Comprehensive Chemical Platforms. These platforms encompass a range of advanced tools, equipment, and technologies that streamline complex chemical processes. From intricate synthesis to precise analysis, our platforms empower chemists and researchers to push boundaries and unlock new frontiers of discovery. With integrated automation, real-time monitoring, and precise control over critical parameters, our platforms offer a holistic solution for ambitious chemical endeavors. Unleash the potential of chemistry with our Comprehensive Chemical Platforms.
3.2. Advanced Comprehensive Mass Spectrometry Systems
Dive into the future of analytical chemistry with our Advanced Comprehensive Mass Spectrometry Systems. Harnessing our innovative modules and cutting-edge ionization technology, these systems deliver unprecedented levels of performance and insight. The heart of our systems lies in a reference database boasting 1.7 billion spatial conformers from 102 million known small molecules (www.multi-d.com). This expansive knowledge base fuels your ability to analyze, identify, and understand complex molecular structures with exceptional accuracy. Step into the realm of advanced mass spectrometry and redefine the boundaries of molecular analysis.
3.3. Unique Positioning and Inspection Systems
Navigate the realms of inspection and exploration like never before with our Unique Positioning and Inspection Systems. These systems are born from the fusion of computer vision, thermal imaging, and gas sensors, offering an autonomous and operator-free solution for inspections in radiation-prone and toxic environments. Equipped with the intelligence to maneuver through challenging industrial spaces, these systems redefine inspection methodologies. Embrace unparalleled efficiency and safety in your inspection processes and pave the way for cost-effective and thorough industrial assessments.
We're always open to discussing your unique challenges and offering solutions customized to you. It's entirely possible that the ideal solution already exists in our repertoire, ready to elevate your business with new levels of efficiency and innovation.
Join Elegant Mathematics and unlock limitless horizons of technical progress. Together, we will breathe life into your boldest ideas.
When It Counts, We Count on Elegant Mathematics
Complex problems don’t need 10,000 lines of code.
They just need the right ten.
That’s where
elegance meets execution — and where we build systems that deliver.
Entdecken Sie unsere Vielzahl von vorgefertigten Lösungen, die höchsten Qualitäts- und technischen Standards gerecht werden.
1. Beschleunigen Sie mit vorgefertigten Lösungen
Minimieren Sie die Entwicklungszeit, indem Sie aus unseren vorgefertigten Lösungen auswählen, die sich innerhalb von nur 3-4 Monaten an Ihre Bedürfnisse anpassen lassen:
1.1. Softwarelösungen für inverse Probleme der Maxwell-Gleichungen
Wir verfügen über umfangreiche Erfahrung in der Lösung inverser Probleme der geometrischen Optik und der Maxwell-Gleichungen. Unser Unternehmen hat spezialisierte Softwarebibliotheken entwickelt, die wir erfolgreich für die Modellierung und Lösung praktischer Probleme einsetzen. Unsere Technologien werden beispielsweise zur Datenverarbeitung in Bodenradaren verwendet, die von unserem Unternehmen entwickelt werden (
https://www.sar-saar.com/), wie in dem Artikel (doi: 10.1109/IWAGPR.2011.5963843) erwähnt.
1.2. Softwarelösungen im Bereich der Strömungsdynamik
Moderne Softwarepakete können laminare oder schwach turbulente Strömungen numerisch vorhersagen, indem sie die Navier-Stokes-Gleichungen diskretisieren. Die Modellierung stark turbulenter Strömungen mit Reynolds-Zahlen über 10000 oder Strömungen mit hohen Knudsen-Zahlen bleibt jedoch eine herausfordernde Aufgabe. Die meisten bestehenden Lösungen erfordern erhebliche Rechenressourcen, was ihre Nutzung selbst auf leistungsstarken Supercomputern einschränkt.
Unsere Methoden zur Lösung der adaptiven Boltzmann-Gleichung unter Verwendung von multilinearen (Tensor-)Approximationen (doi: 10.1007/s00607-002-1458-9, 10.1002/pamm.200700641, 10.1002/pamm.200700839) ermöglichen die Modellierung physikalischer Prozesse, die für die Navier-Stokes-Gleichungslöser unzugänglich sind. Diese Methoden sind effektiv bei der Modellierung von Strömungen mit unterschiedlichen Geschwindigkeitsrichtungen oder Durchschnittstemperaturen auf kurzen Distanzen.
Unsere Lösungen werden für Aufgaben wie die Vorhersage der Form von Turbomolekularpumpen-Schaufeln (bis zu 10
-12 Torr), die Optimierung von Massen-Spektrometertraktaten (bis zu 10
-10 Torr), die Vorhersage der Formen von HPLC/UHPLC-Ventilen (1000-5000 Bar), die Optimierung von chemischen Reaktorformen, einschließlich solcher mit überkritischen Flüssigkeiten, und anderen komplexen Aufgaben eingesetzt, bei denen traditionelle numerische Methoden nicht die erforderliche Genauigkeit bieten.
1.3. Module für automatisierte Mikroskopie und biologische Analyse
Entdecken Sie die verborgenen Details biologischer Proben mit unseren modernen Modulen für automatisierte Mikroskopie. Diese Module integrieren fortschrittliche Bildgebungstechnologie mit leistungsstarker statistischer Analyse und ermöglichen es Ihnen, wertvolle Erkenntnisse aus komplexen biologischen Proben zu gewinnen. Von der Analyse der Partikelgrößenverteilung bis zu komplexen statistischen Auswertungen ermöglichen Ihnen unsere Module, die Grenzen der wissenschaftlichen Entdeckung zu erweitern. Lassen Sie unsere Technologie die mikroskopische Welt erhellen und ihre Geheimnisse enthüllen.
1.4. Automatische Probenehmer
Möchten Sie den Umgang mit Proben in Ihrem Labor optimieren? Unsere automatischen Probenehmer sind sorgfältig entwickelt, um Effizienz und Genauigkeit in Ihrem Laborworkflow zu steigern. Diese automatisierten Systeme sind in der Lage, eine Vielzahl von Probentypen und -größen zu verarbeiten. Durch präzise Automatisierung gewährleisten wir konsistente und reproduzierbare Ergebnisse, wodurch menschliche Fehler erheblich reduziert und wertvolle Zeit für Ihr Team freigesetzt wird. Egal, ob in den Bereichen Chemie, Biologie oder darüber hinaus - unsere automatischen Probenehmer bringen ein neues Maß an Präzision in Ihre wissenschaftlichen Unternehmungen.
1.5. Steuerungsmodule für Turbomolekularpumpen
Im Bereich der Vakuumtechnologie stehen unsere Steuerungsmodule für Turbomolekularpumpen für Präzision und Kontrolle. Diese Module bieten umfassendes Management turbomolekularer Pumpen und gewährleisten optimale Leistung und Lebensdauer. Mit ausgefeilten Algorithmen und Echtzeitüberwachung regeln diese Module Druck, Temperatur und andere wichtige Parameter und erhalten so eine stabile und kontrollierte Vakuumumgebung. Erleben Sie Höchstleistung und Zuverlässigkeit in Ihren Vakuumsystemen mit unseren Steuerungsmodulen für Turbomolekularpumpen.
1.6. Präzisions-Spannungsregelung für Massenspektrometer
Heben Sie Ihre Massenspektrometrie-Experimente auf beispiellose Genauigkeit mit unseren Präzisions-Spannungsregelungsmodulen. Mit der Fähigkeit zur präzisen Manipulation der Spannung im Mikrosekundenbereich definieren diese Module die Möglichkeiten Ihrer Massenspektrometer neu. Mit programmierbarer Wellenformgestaltung und Synchronisation über mehrere Kanäle ermöglicht Ihnen unsere Technologie außergewöhnliche Präzision bei Ionisierungsprozessen. Übernehmen Sie die Kontrolle über Ihre Experimente mit größtem Vertrauen und Präzision.
1.7. Metalloxidsensorbasierte Überwachungssysteme
Schützen Sie Ihre industriellen Räume und Operationen mit unseren metalloxidsensorbasierten Überwachungssystemen. Diese modernen Systeme verwenden fortschrittliche Metalloxidsensoren, um industrielle Gase und Lecks in Echtzeit zu erkennen und zu identifizieren. Von der Überwachung der Gaskonzentration bis zur schnellen Identifizierung gefährlicher Substanzen verbessern unsere Überwachungssysteme die Arbeitssicherheit und die Umweltverträglichkeit. Gewinnen Sie Echtzeit-Einblicke und stellen Sie eine sichere Arbeitsumgebung mit unseren metalloxidsensorbasierten Überwachungssystemen sicher.
2. Schlüssellösungen für ambitionierte Ziele
Für umfangreichere Anforderungen stehen unsere Produkte innerhalb von 6-8 Monaten zur Verfügung, sorgfältig auf Ihre anspruchsvollen Anforderungen zugeschnitten:
2.1. Hochspannungsblöcke für Radiochemie
Unternehmen Sie Projekte, die beispiellose Präzision und Kontrolle über Hochspannungsprozesse erfordern? Unsere Hochspannungsblöcke für Radiochemie sind darauf ausgelegt, die anspruchsvollsten Anforderungen Ihrer radiochemischen Anwendungen zu erfüllen. Mit Spannungsbereichen von bis zu 100 kV gewährleisten diese spezialisierten Blöcke eine zuverlässige und stabile Leistung unter extremen Bedingungen. Ob in der Kernforschung, Teilchenbeschleunigung oder experimentellen Aufbauten, die Hochspannungsbausteine verleihen Ihren Vorhaben einen entscheidenden Vorteil. Verlassen Sie sich auf unsere Expertise, um die Hochspannungslösungen zu liefern, die Sie für Ihren Erfolg benötigen.
2.2. Mechanische Antriebs- und Steuersysteme
Von der Chromatographie bis zur Massenspektrometrie liegt das Herz der Präzision in der sorgfältigen mechanischen Steuerung. Unsere mechanischen Antriebs- und Steuersysteme bieten eine Symphonie der Präzisionsingenieurkunst und ermöglichen es Ihnen, Bewegungen mit höchster Genauigkeit zu orchestrieren. Diese Systeme integrieren sich nahtlos in verschiedene wissenschaftliche Instrumente und bieten reibungslose und zuverlässige mechanische Antriebe für vielfältige Anwendungen. In Verbindung mit anspruchsvoller Steuerungssoftware geben Ihnen unsere Systeme die Möglichkeit, experimentelle Aufbauten mühelos feinzutunen und zu optimieren. Steigern Sie Ihre mechanische Präzision und starten Sie eine neue Ära der experimentellen Meisterschaft.
3. Mutig die Zukunft mit uns gestalten
In 12 bis 15 Monaten bieten wir integrierte Lösungen, die in der Lage sind, Ihr Unternehmen wirklich zu transformieren:
3.1. Umfassende chemische Plattformen
Erleben Sie Chemie auf einer völlig neuen Ebene mit unseren umfassenden chemischen Plattformen. Diese Plattformen umfassen eine Reihe fortschrittlicher Werkzeuge, Ausrüstungen und Technologien, die komplexe chemische Prozesse optimieren. Von aufwendiger Synthese bis hin zur präzisen Analyse ermöglichen unsere Plattformen Chemikern und Forschern, Grenzen zu überschreiten und neue Entdeckungsbereiche zu erschließen. Mit integrierter Automatisierung, Echtzeitüberwachung und präziser Kontrolle über kritische Parameter bieten unsere Plattformen eine ganzheitliche Lösung für ambitionierte chemische Vorhaben. Entfesseln Sie das Potenzial der Chemie mit unseren umfassenden chemischen Plattformen.
3.2. Fortgeschrittene umfassende Massenspektrometriesysteme
Tauchen Sie ein in die Zukunft der analytischen Chemie mit unseren fortgeschrittenen umfassenden Massenspektrometriesystemen. Mit unseren innovativen Modulen und modernster Ionisationstechnologie bieten diese Systeme unerreichte Leistung und Einblicke. Das Herz unserer Systeme ist eine Referenzdatenbank mit 1,7 Milliarden räumlichen Konformern aus 102 Millionen bekannten kleinen Molekülen (www.multi-d.com). Diese umfangreiche Wissensbasis ermöglicht es Ihnen, komplexe molekulare Strukturen mit außergewöhnlicher Genauigkeit zu analysieren, zu identifizieren und zu verstehen. Betreten Sie die Welt der fortschrittlichen Massenspektrometrie und definieren Sie die Grenzen der molekularen Analyse neu.
3.3. Eindeutige Positionierungs- und Inspektionssysteme
Navigieren Sie wie nie zuvor durch die Bereiche Inspektion und Erkundung mit unseren einzigartigen Positionierungs- und Inspektionssystemen. Diese Systeme entstehen aus der Fusion von Computer Vision, Thermografie und Gassensoren und bieten eine autonome und bedienerfreie Lösung für Inspektionen in strahlengefährdeten und giftigen Umgebungen. Ausgestattet mit der Intelligenz, sich durch anspruchsvolle industrielle Räume zu bewegen, definieren diese Systeme Inspektionsmethoden neu. Nutzen Sie unerreichte Effizienz und Sicherheit in Ihren Inspektionsprozessen und bahnen Sie den Weg für kostengünstige und gründliche industrielle Bewertungen.
Wir sind immer offen für die Diskussion Ihrer einzigartigen Herausforderungen und bieten maßgeschneiderte Lösungen für Sie an. Es ist durchaus möglich, dass die ideale Lösung bereits in unserem Repertoire existiert und bereit ist, Ihr Unternehmen mit neuen Maßstäben in Effizienz und Innovation zu bereichern.
Treten Sie Elegant Mathematics bei und entfesseln Sie grenzenlose Horizonte des technischen Fortschritts. Gemeinsam werden wir Ihre kühnsten Ideen zum Leben erwecken.
Elegant Mathematics: A 20-Year Journey of Innovation
Equations Solved. Systems Built. Challenges Met.
Elegant Mathematics represent an exceptional company specializing in contract R&D and the production of high-tech solutions in the fields of chemistry, physics, and computer science. For over two decades,
Elegant Mathematics has transformed
cutting-edge mathematical research into deployable technologies.
Our breakthroughs include a
revolutionary approach to
computational fluid dynamics based on the
Boltzmann equation, enabling
high-fidelity simulations in
extreme regimes. We’ve developed a
fully autonomous flying wing for exploration in
GPS-denied environments, created
advanced systems for sensor fusion and
embedded AI, and engineered
software solutions for
inverse problems of Maxwell’s equations. Our expertise extends into
chemistry as well — with innovations in
comprehensive mass spectrometry and a portfolio of
five U.S. patents protecting our
core technologies.
Since 2006, we have been at the forefront of this industry, with our origins dating back to 1991 when our American office received its first order from Cray Research Inc for the development of rapid parallel algorithms for solving systems with sparse matrices.
From our inception, we have been actively engaged in contract software development and electronic equipment component design. Our achievements
encompass successful collaborations with prominent companies such as ExxonMobil, Sodern, NXP, Western Atlas, Robert Bosch GmbH, Northrop Grumman,
and Nvidia. We conduct contract research and development for corporate clients, prestigious European universities, and research centers,
spanning diverse areas of science and technology.
Key Areas of Expertise:
- Computer Vision: Crafting cutting-edge computer vision systems for various applications.
- Scientific Electronics: Creating precision scientific electronics capable of tackling intricate challenges.
- Software Development: Engineering software solutions for scientific equipment, industrial electronics, and analytical chemistry.
Elegant Mathematics: 20 Jahre Innovation im Einsatz
Gleichungen gelöst. Systeme gebaut. Herausforderungen gemeistert.
Elegant Mathematics repräsentiert ein außergewöhnliches Unternehmen, das sich auf Vertragsforschung und die Herstellung von High-Tech-Lösungen in den Bereichen Chemie, Physik und Informatik spezialisiert hat. Seit
über zwei Jahrzehnten verwandelt Elegant Mathematics
wegweisende mathematische Forschung in einsatzfähige Technologien.
Zu unseren Durchbrüchen zählt ein
revolutionärer Ansatz in der
numerischen Strömungsmechanik auf Basis der
Boltzmann-Gleichung, der
hochpräzise Simulationen unter
extremen physikalischen Bedingungen ermöglicht. Wir haben ein
vollständig autonomes Nurflügelsystem für Erkundungsmissionen in
GPS-freien Umgebungen entwickelt,
fortschrittliche Lösungen für Sensorfusion und
eingebettete KI realisiert sowie spezialisierte
Software für
inverse Probleme der Maxwell-Gleichungen entworfen.
Unsere Expertise reicht auch in die
Chemie hinein – mit Innovationen in der
umfassenden Massenspektrometrie und einem Portfolio von
fünf US-Patenten, die unsere
Schlüsseltechnologien schützen.
Seit 2006 stehen wir an der Spitze dieser Branche, wobei unsere Wurzeln bis ins Jahr 1991 zurückreichen, als unser amerikanisches Büro den ersten Auftrag von Cray Research Inc zur Entwicklung schneller paralleler Algorithmen zur Lösung von Systemen mit dünnen Matrizen erhielt.
Von Anfang an waren wir aktiv in der Vertragssoftwareentwicklung und im Design von elektronischen Gerätekomponenten tätig. Zu unseren Erfolgen gehören erfolgreiche Zusammenarbeiten mit namhaften Unternehmen wie ExxonMobil, Sodern, NXP, Western Atlas, Robert Bosch GmbH, Northrop Grumman und Nvidia. Wir führen Vertragsforschung und -entwicklung für Unternehmenskunden, renommierte europäische Universitäten und Forschungszentren in verschiedenen Bereichen von Wissenschaft und Technologie durch.
Schlüsselkompetenzbereiche:
- Computer Vision: Entwicklung hochmoderner Computersichtsysteme für verschiedene Anwendungen.
- Wissenschaftselektronik: Entwicklung präziser wissenschaftlicher Elektronik, die in der Lage ist, komplexe Herausforderungen zu bewältigen.
- Softwareentwicklung: Entwicklung von Softwarelösungen für wissenschaftliche Geräte, industrielle Elektronik und analytische Chemie.
Our Engagements
 | |
Presenting the emRadiant portable mini-system: Experience advanced SLAM capabilities and seamless sensor integration at your fingertips! Whether you are engaged in robotics, mobile platforms, vehicle automation, or industrial machinery, this cutting-edge technology is equally suitable for aerial vehicles, drones, UAVs, security systems, and beyond. Elevate your robotic observations to new heights with the emRadiant!
|
 | |
Introducing the Elegant NMR® System with Elmathron®: This revolutionary system redefines affordability and simplicity, democratizing NMR as an accessible analytical method for chemistry laboratories. Harness the power of DNP NMR to gain new insights into chemical analysis!
|
 | |
Presenting SAR-SAAR: Discover the precision of three-dimensional underground scanning, seamlessly aligned with three-dimensional imagery and geodetic coordinates.
|
We are dedicated to impactful social initiatives
 | |
Introducing MR NIB™: A compact, portable MRI device that leverages the DNP enhancement method for state-of-the-art health monitoring. This technology is safeguarded by multiple US patents, offering an affordable, swift, and precise solution.
|
 | |
Presenting HugeMDB: The world's largest molecular database, housing approximately 102 million molecules and roughly 1.7 billion spatial structures! Accessing the search program is completely free and requires no special user registration.
|
Unsere Engagements
 | |
Vorstellung des tragbaren Mini-Systems emRadiant: Erleben Sie fortschrittliche SLAM-Fähigkeiten und nahtlose Integration von Sensoren direkt an Ihren Fingerspitzen! Ob Sie in den Bereichen Robotik, mobile Plattformen, Fahrzeugautomatisierung oder industrielle Maschinen tätig sind, diese wegweisende Technologie eignet sich gleichermaßen für Luftfahrzeuge, Drohnen, UAVs, Sicherheitssysteme und vieles mehr. Heben Sie Ihre robotischen Beobachtungen mit dem emRadiant auf ein neues Niveau!
|
 | |
Stellen Sie das Elegant NMR®-System mit Elmathron® vor: Dieses revolutionäre System definiert die Erschwinglichkeit und Einfachheit neu und macht NMR als zugängliche analytische Methode für Chemielabore zugänglich. Nutzen Sie die Kraft von DNP NMR, um neue Erkenntnisse in der chemischen Analyse zu gewinnen!
|
 | |
Entdecken Sie SAR-SAAR: Die Präzision dreidimensionaler Untergrundscans, nahtlos integriert mit dreidimensionalem Imaging und geodätischen Koordinaten.
|
Wir engagieren uns für wirkungsvolle soziale Initiativen
 | |
Stellen Sie MR NIB™ vor: Ein kompaktes, tragbares MRT-Gerät, das die DNP-Verstärkungsmethode für hochmoderne Gesundheitsüberwachung nutzt. Diese Technologie ist durch mehrere US-Patente geschützt und bietet eine erschwingliche, schnelle und präzise Lösung.
|
 | |
Präsentieren Sie HugeMDB: Die weltweit größte molekulare Datenbank mit etwa 102 Millionen Molekülen und etwa 1,7 Milliarden räumlichen Strukturen! Der Zugriff auf das Suchprogramm ist völlig kostenlos und erfordert keine spezielle Benutzerregistrierung.
|
Our Resources Encompass:
Integrated Production Cycle: We offer a complete cycle of electronic development, manufacturing, and testing.

We design and develop our own boards. We have reliable printed circuit board suppliers who can deliver fully manufactured boards to our German office within just one day after receiving the electronic drawings (Gerber files).
As regular customers of global electronic network stores such as Mouser, DigiKey, Farnell, Newark, RsComponents, TI, Microchip, we receive electronic components within 1-2 working days, allowing us to assemble printed circuit boards at our in-house production facilities.
Our state-of-the-art component placement machines and reflow ovens enable us to rapidly assemble electronics, reducing our reliance on external assembly service providers. Even without scaling up production, we can assemble several square meters of printed circuit boards daily.
We specialize in designing and assembling complex electronics.
In some of our devices, the total area of printed circuit boards can reach up to 10 square meters, with over 20,000 components.
Advanced Laboratories: We have a well-equipped chemical laboratory where virtually any synthesis can be conducted, and the results of this synthesis can be used for measuring physical and chemical properties.
Even during synthesis, we can perform measurements thanks to our chemical analysis laboratory features a wide range of customizable analytical equipment, which includes analytical and preparative chromatographs, mass spectrometers, chromatography-mass spectrometry instruments, tabletop NMR, and devices for measuring various types of spectra ranging from 20 nm to 7 µm. Additionally, we have well-equipped optical microscopes with brightfield, darkfield, polarization, and fluorescent options, offering magnification of up to 2500 times.
Within our laboratory, a comprehensive inventory of spare parts, connectors, and components is readily available, facilitating rapid prototyping, research, and precise small-scale production. Our well-maintained stock guarantees the successful resolution of any technical challenges.
Moreover, our laboratory boasts high-pressure systems (up to 1600 bar) and deep vacuum systems (down to 10
-12 Torr), empowering us to undertake measurements and prototyping for the most complex technical hurdles.
Mechanical Assembly Technologies: We possess modern CNC equipment for mechanical assembly.
Supercomputing Power: Our supercomputer with 24 TB of RAM can efficiently tackle even the most complex tasks. Collaborating with Nvidia and being recognized as
official Nvidia CUDA consultants, we always have access to the world's most powerful supercomputers.
Unsere Ressourcen umfassen:
Integrierter Produktionszyklus: Wir bieten einen kompletten Zyklus der Elektronikentwicklung, -herstellung und -prüfung an.

Wir entwerfen und entwickeln unsere eigenen Platinen. Wir haben zuverlässige Lieferanten für gedruckte Leiterplatten, die vollständig hergestellte Platinen an unser deutsches Büro liefern können, nur einen Tag nach Erhalt der elektronischen Zeichnungen (Gerber-Dateien).
Als regelmäßige Kunden globaler Elektroniknetzwerk-Shops wie Mouser, DigiKey, Farnell, Newark, RsComponents, TI und Microchip erhalten wir elektronische Komponenten innerhalb von 1-2 Arbeitstagen, was es uns ermöglicht, gedruckte Leiterplatten in unseren eigenen Produktionsstätten zu montieren.
Unsere hochmodernen Bauteileinsetzmaschinen und Reflow-Öfen ermöglichen es uns, Elektronik schnell zusammenzubauen und unsere Abhängigkeit von externen Montagedienstleistern zu reduzieren. Selbst ohne eine Produktionssteigerung können wir täglich mehrere Quadratmeter gedruckte Leiterplatten montieren.
Wir sind auf das Design und die Montage komplexer Elektronik spezialisiert.
In einigen unserer Geräte kann die Gesamtfläche der gedruckten Leiterplatten bis zu 10 Quadratmeter erreichen, mit über 20.000 Komponenten.
Modernste Laboratorien: Wir verfügen über ein gut ausgestattetes chemisches Labor, in dem praktisch jede Synthese durchgeführt werden kann, und die Ergebnisse dieser Synthese können zur Messung physikalischer und chemischer Eigenschaften verwendet werden.
Selbst während der Synthese können wir Messungen durchführen, dank unseres chemischen Analyselabors, das eine breite Palette an anpassbarer Analysegeräten umfasst, darunter analytische und präparative Chromatographen, Massenspektrometer, Chromatographie-Massenspektrometrie-Geräte, Tisch-NMR und Geräte zur Messung verschiedener Arten von Spektren von 20 nm bis 7 µm. Darüber hinaus verfügen wir über gut ausgestattete optische Mikroskope mit Brightfield, Darkfield, Polarisation und fluoreszierenden Optionen, die eine Vergrößerung von bis zu 2500-fach bieten.
In unserem Labor steht stets ein umfangreicher Bestand an Ersatzteilen, Verbindern und Komponenten zur Verfügung, was eine schnelle Prototypenentwicklung, Forschung und präzise Kleinserienproduktion ermöglicht. Unser gut gepflegter Lagerbestand garantiert die erfolgreiche Bewältigung jeglicher technischer Herausforderungen.
Darüber hinaus verfügt unser Labor über Hochdrucksysteme (bis zu 1600 bar) und Vakuumsysteme (bis zu 10
-12 Torr), was uns befähigt, Messungen und Prototypenentwicklungen für die komplexesten technischen Herausforderungen durchzuführen.
Mechanische Montagetechnologien: Wir verfügen über moderne CNC-Ausrüstung für die mechanische Montage.
Supercomputing-Leistung: Unser Supercomputer mit 24 TB RAM kann selbst die komplexesten Aufgaben effizient bewältigen. In Zusammenarbeit mit Nvidia und der Anerkennung als
offizielle Nvidia CUDA-Berater haben wir immer Zugang zu den leistungsstärksten Supercomputern der Welt.
News
July, 2025:
Elegant Mathematics is proud to announce that our
pitch video, ML-Tensor-Boltzmann Approach for Revolutionizing Computational Fluid Dynamics, scored an impressive
86.5/100 and has achieved
“Awardable” status through
DARPA Expedited Research Implementation Series (ERIS) Marketplace.
This recognition highlights our innovation, scalability, and potential to transform DoD missions in a highly competitive field.
Learn more at
darpaconnect.us/eris.
May, 2025:
Our paper titled
"Methods for Localization and Identification of Casualties in Mass Disaster Areas Using Multimodal Sensors" has recently been accepted for presentation at the
Military Health System Research Symposium.
We are honored and excited to share our findings at this prestigious international forum on military medicine.
March, 2025:
We are open to collaboration for the FBI project on Endless Generative Waveforms. Further details can be found on
the END-GEN project website at FBI, and information about our methods, algorithms, and approaches can be found on our website
https://www.sar-saar.com/.
November, 2024:
Our Elegant Mathematics Team, aka
MR NIB, is now part of the
Systems Competition Teams (year 2) in the
DARPA Triage Challenge (DTC) - the most renowned worldwide competition in military medicine, held every three years!
We're thrilled about this opportunity and can't wait to dive into the challenge. Stay tuned for updates!
The most detailed news archive can always be found on our company’s news feed on
LinkedIn and on our
CTO’s page.
Nachrichten
Juli, 2025:
Elegant Mathematics is proud to announce that our
pitch video, ML-Tensor-Boltzmann Approach for Revolutionizing Computational Fluid Dynamics, scored an impressive
86.5/100 and has achieved
“Awardable” status through
DARPA Expedited Research Implementation Series (ERIS) Marketplace.
This recognition highlights our innovation, scalability, and potential to transform DoD missions in a highly competitive field.
Learn more at
darpaconnect.us/eris.
Mai, 2025:
Unser Vortrag mit dem Titel
„Methoden zur Lokalisierung und Identifizierung von Verletzten in Katastrophengebieten mithilfe multimodaler Sensoren“ wurde kürzlich für das
Military Health System Research Symposium angenommen.
Wir freuen uns sehr darauf, unsere Ergebnisse auf diesem renommierten internationalen Symposium für Militärmedizin präsentieren zu dürfen.
März 2025:
Wir sind offen für eine Zusammenarbeit im FBI-Projekt zur Endless Generative Waveforms. Weitere Details finden Sie auf der
END-GEN-Projektseite beim FBI und Informationen über unsere Methoden, Algorithmen und Ansätze auf unserer Website
https://www.sar-saar.com/.
November 2024
Unser Elegant Mathematics-Team, auch bekannt als
MR NIB, ist jetzt Teil der
Systems Competition Teams (Jahr 2) bei der
DARPA Triage Challenge (DTC) – dem weltweit renommiertesten Wettbewerb in der Militärmedizin, der alle drei Jahre stattfindet!
Wir freuen uns über diese Gelegenheit und können es kaum erwarten, uns in die Herausforderung zu stürzen. Bleiben Sie dran für Updates!
Das detaillierteste Nachrichtenarchiv finden Sie immer im Nachrichtenfeed unseres Unternehmens auf
LinkedIn und auf der Seite unseres
CTOs.
Contact Us Today
Kontaktieren Sie uns heute
Our technical support and information office is always available for you.
Unser technischer Support und Informationsbüro ist jederzeit für Sie erreichbar.
We are committed to providing the best possible solutions for our customers.
Wir sind bestrebt, unseren Kunden die bestmöglichen Lösungen anzubieten.
To place orders, please schedule a video chat with us on
Calendly.
Alternatively, feel free to reach out to us via our corporate email address. We guarantee a response within 24 hours and may request additional information if needed.
Um Bestellungen aufzugeben, vereinbaren Sie bitte einen Video-Chat mit uns auf
Calendly.
Alternativ können Sie sich gerne über unsere Unternehmens-E-Mail-Adresse an uns wenden. Wir garantieren eine Antwort innerhalb von 24 Stunden und können bei Bedarf weitere Informationen anfordern.
82834, WY, USA
Tel: +1 (631) 729 - 8304
Email: info at elegant - mathematics dot com
Elegant Mathematics Ltd
Hanauer Muehle 2,
66564, Ottweiler-Fuerth,
Saarland, Germany
Tel: +49 (6858) 98 90 92 4
Email: info at elegant - math dot de
Legal registration numbers:
USA: Cheyenne 746213
UK: Cardiff 05975337
DE: HRB 16570
Rechtliche Registrierungsnummern:
USA: Cheyenne 746213
UK: Cardiff 05975337
DE: HRB 16570
Active and registered since 23 Oct 2006
German tax payer's account number 030/146/00565
EU VAT account number DE 257663693
CAGE/NCAGE (US and NATO Commercial and Government Entity): CNDX2
SAM.GOV UNIQUE ENTITY ID: J1ZZCN4F9PB9
Aktiv und registriert seit dem 23. Oktober 2006
Deutsche Steuerzahlerkontonummer 030/146/00565
EU-Umsatzsteuerkontonummer DE 257663693
CAGE/NCAGE (US and NATO Commercial and Government Entity): CNDX2
SAM.GOV UNIQUE ENTITY ID: J1ZZCN4F9PB9
Elegant Mathematics technologies are protected by a plurality of patents and pending patent applications!
Die Technologien von Elegant Mathematics sind durch eine Vielzahl von Patenten und anhängigen Patentanmeldungen geschützt!
Disclaimer: By providing links to other sites, Elegant Mathematics Ltd, and Elegant Mathematics LLC do not guarantee, approve, or endorse
the information or products available at those sites, nor does a link indicate any association with or endorsement by the linked site of
elegant-mathematics.com or elegant-mathematics.de.
Haftungsausschluss: Durch die Bereitstellung von Links zu anderen Websites garantieren, genehmigen oder unterstützen Elegant Mathematics Ltd
und Elegant Mathematics LLC nicht die Informationen oder Produkte, die auf diesen Websites verfügbar sind. Ein Link bedeutet auch keine Verbindung
oder Billigung durch die verlinkte Website von elegant-mathematics.com oder elegant-mathematics.de.